End of the blog

Over the past decade the main aim of this blog has been to force me to follow at least a little bit of recent mathematical ideas and news, despite being fairly far from academia myself.

It did work to some extent, but with a new job in Paris on the horizon I feel I’ll finally have more opportunities to attend seminars and meet folks than in the past. Therefore now is the right time to stop blogging. Thank you to all those who provided insightful comments over the years.

by Fondo Antiguo de la Biblioteca de la universidad de Sevilla on flickr

Séminaire Betty B. and other short news

[Posted on february 20, 2018.]

The first Séminaire Betty B., after the name of a granddaughter of Nicolas Bourbaki [edit: see this blog post by Lieven Le Bruyn for context ; I’ve noticed she has a twitter account too], will take place next march at École Normale Supérieure. An interesting novelty indeed! As for the next Séminaire Bourbaki of march 31, Jean-Pierre Serre, 91, will be one of the speakers.

Still on the topic of Women in Maths, there’s an open column by Indira Chatterji in the january 2018 issue of Gazette des mathématiciens, which is an important read, as least for folks working in France (keywords: #metoo, glass ceiling). That issue also has an interesting dossier on ethics in research (in particular in editorial committees).

On an entirely different topic, Jean-Yves Girard released at the end of last year a paper titled “La Logique 2.0”, which is an extremely interesting leap from his previous works. I cannot claim to understand most of it, but I now see much clearer what he was aiming at, truly inspiring! The core is the 4-fold Constat/Performance/Usine/Usage structure of proofs that he describes. A byproduct is the occurence of two new propositional constants that are self-dual and allow one to turn integers into propositions, i.e. consequences from something deeper, and so too the Peano axioms. This is made possible by a notion of truth, very far from Tarki’s, involving a topological concept : the Euler-Poincaré characteristic of the graph underlying the proof. It looks pleasingly algebraic too, and is not the final step in his quest since the paper makes it clear that some more technical aspects are still being investigated (namely the extrinsic constraints on the mould, see page 15).

As a final piece of independent news, if you are between 16 and 20 and interested in mathematics, please note the march 31 deadline to apply to the fine Summer School titled Mathematical Summer in Paris, which will take place at École Normale Supérieure next july!

The curious butterfly.

Fougères, october 2017. Public domain.

Some ArXiv stats for 2017

[Posted on december 29, 2017.]

Since the last batch of preprints on the arXiv got out today (european time, at least) here are a few things I’ve noticed in 2017.

The 5th digit for monthly paper numbers was used several times, the precise numbers being : january=9186, february=8910,  march=11008, april=9029, may=11194, june=10297, july=9980, august=9854, september=10517, october=11627, november=11589, december=10011.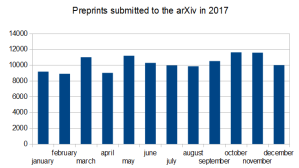

That’s a grand total of 123,202 papers in 2017. Sadly the number of different authors is not easily obtainable.

There were 113,380 submissions in 2016, so it’s an 8.66% increase this year. The increase from 2015 to 2016 had been of 7.69%, but since two new sections (Economics, and Electrical engineering & Systems Science) were started last september, that’s not directly comparable.

See also this page for an official graph of monthly submissions starting in 1994, while monthly download rates are equally fascinating (note the spike this very december!).

Assuming individual authors between 2015 and 2017 had on average a stable number of yearly submissions (of course giving, for a given author, a weight of 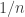to his papers with 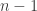coauthors), this would imply an increase of about 8% new authors both in 2016 and 2017.

Who are they? Surely new PhD students for some part, but there are also folks who stopped publishing after obtaining their PhD two years ago, so the 8% figure is a balance between those two populations.  This should be compared to an in-depth count of PhD offers worldwide over the past few years to confirm this scenario, but I don’t have the time to do it.

Should this fail (i.e. offers of PhD didn’t grow much between 2014 and 2016) then probably the initial assumption is incorrect, which would mean authors in fact are publishing more on average. I do wonder which alternative is the correct one…

[Edit (january 3): the official 2017 stats are now out.]

 Winter solstice sunset over Antler Peak,

by Yellowstone National Park on flickr

Some december 2017 news

[Posted on december 4, 2017.]

In no particular order :

• the paper of Mohan Ganesaligam and Sir Timothy Gowers appeared earlier this year in the Journal of Automated Reasoning (ironically, a Springer journal in which it appears they had to pay an APC to have it ‘open access’). Looking at papers which cite it I’ve stumbled upon ALEXANDRIA, a EU-funded project lead by Lawrence C. Paulson. There is in particular a detailed description of actions which shows that, if I understand well, while it finds the human-legible aspect of the G&G paper interesting, it finds the use of formal libraries important, and will directly in result in stuff usable in Isabelle. Lawson’s PhD student Wenda Li has several interesting formal proofs papers, again in the context of Isabelle.  Another paper citing G&G is this one by Joseph Corneli et al., which also looks extremely interesting and from an entirely different angle! If only days had 48 hours…
• the Prizes season is in full swing. The 2018 Breakthrough Prizes have been announced : Christopher Hacon and James McKerman are the laureates for their work on the minimal model program (which previously earned them the Cole Prize in Algebra among others ; incidentally, this Cole Prize has just been won by Robert Guralnik this year). Also, 4 New Horizons in Mathematics Prizes went to Aaron Naber  (see e.g. this 3 part video on Yang-Mills Theory : part1 part2 part3), Maryna Viasovska (topically, Henry Cohn won the Conant Prize for his paper on the sphere packings story), Zhiwei Yun and Wei Zhang (both for their Annals of Mathematics paper in particular, see also Quanta Magazine).
• the Fermat Prize went to Simon Brendle and to Nader Masmoudi.
• Physicist Slava Rychkov (currently at ENS) has been named permanent professor at IHES
• Edward Frenkel announced two weeks ago that Shinichi Mochizuki had sent the final versions of his papers for approval. I think I saw it said that it had been submitted to a Japanese journal, but this is probably not Pub. RIMS since Mochizuki himself seems to serve as its editor-in-chief. Time will tell…
• Christie’s will look to sell next week for at least USD10,000 a 1952 copy of the issue of Phil. Trans. Roy. Soc. which contains Turing’s paper on morphogenesis
• if you are a mathematics student in France, you should go to the Forum Emploi Math next week.

Peacock dance display, by Marco Verch on flickr

Some november 2017 items

[Posted on november 11, 2017]

Some recently spotted items :

• Simon Brendle’s work giving higher dimensional generalisations of the work of Hamilton and Perelman will appear in Annals of Mathematics.
• an apparently fundamental object in p-adic Hodge theory is a curve due to Laurent Fargues and Jean-Marc Fontaine. Fargues will give his ICM talk La courbe on this (and gave a Masters course on it 3 years ago). For other aspects, in particular historical ones, there is Pierre Colmez’s preface of a book. A workshop took place on this in its early days at ENS. Some notes of Xavier Caruso from 2015 are here, while Peter Scholze’s ARGOS focussed on it. A very recent item in english on the topic are these notes by Timo Richarz.
• please consider making a donation to MO (if you do through the paypal thing, make sure you fill in the form completely, otherwise it erases your card number, asks again, and goes to the double captcha again…)
• the Séminaire Lectures Grothendieckiennes recently began at ENS.
• Alain Connes has become emeritus professor at Collège de France and ceased to teach, while Stéphane Mallat will start a new Chaire de Science des Données in january. This means the Mathématiques et Sciences du Numérique section (previously Mathématiques only) is now made of two math Chairs (Pierre-Louis Lions and Claire Voisin) and two computer science ones (Gérard Berry and Mallat) while Claire Matthieu will give shortly her inaugural lecture on Algorithms as part of her 1-year Chair (the same type of fixed-term Chair given to Yann LeCun two years ago).
• the videos of the Claymath conference of last september are now online with several great Colloquium-style talks!
• the great diamond OA Journal of Machine Learning Research has a nice little feature : acceptance statistics.

Hexagons in the arch. Glanum, october 2017. Public Domain.

Some october 2017 news

[Posted on october 12, 2017]

Some recent news :

• Vladimir Voevodsky’s death has been a shock to many, see IAS resources here (including the video of the Remembrance Gathering), see also a Quanta Magazine article of yesterday
• a very new generalist Diamond OA journal is proposed by ENS de Rennes under the name Annales Henri Lebesgue, it has a strong editorial board and no accepted papers just yet (I’ve learnt about its existence while browsing  the program of an upcoming conference of Réseau National des Bibliothèques de Mathématiques)
• Misha Gromov put yesterday on the arXiv a long paper, and finishes it with the sentence “Non-accessible Articles. There is a dozen or so other papers on Gehring linking problem but, since they are not openly accessible, one can not tell what is written in there.” If that type of statement generalizes that could quickly make the guilty authors consider arXiving their work…
• Astrophysicist Konstantin Batygin has teamed up with Dynamical Systems expert Alessandro Morbidelli to release a beautiful paper that adds a good theoretical underpinning to the Planet Nine hypothesis
• Giovanni Coppola has recently claimed a conditional proof of the Twin Prime Conjecture (among others) based on a Delange Hypothesis

The Genestier-V.Lafforgue preprint is out, and V.Lafforgue’s crypto-currency proposal for refereeing

[Posted on september 6, 2017.]

Alain Genestier and Vincent Lafforgue have very recently posted a preprint which is the long-awaited follow-up to V.Lafforgue’s 2012 paper on the Langlands Correspondance (whose current version of august 2017 seems to be close to print, since it acknowledges the “extremely thorough” input from several referees).

On V.Lafforgue’s webpage there is a very interesting note from january 2017 titled A proposition to give value to the work of referees which introduces the idea of a crypto-currency to reward referees (!), provides concrete technical specifications to implement and test the idea, and explores potential drawbacks.

I haven’t seen it discussed on the web yet, but I very much hope it will become widely read, and that a suitable version will emerge and be given a try by several large institutions…

Programmer’s laptop by Wall Boat on flickr

Early september 2017 items

[Posted on september 3, 2017.]

Various short news :

• Go Yamashita has posted a few days ago his version of Shinichi Mochizuki’s work on the abc conjecture (and he also has posted an excerpt of an email which, together with a footnote, alludes to some unethical behaviour from a certain I.F. Hopefully, whether or not it is the case, this type of controversy will stay away from the math itself.)
• the arXiv overlay journal Épiga has finally released its first papers
• it has been announced today that the french Secretary of State in Digital Affairs, Mounir Mahjoubi, has asked Cédric Villani to write a report on how France should define a strategy for the coming years regarding the rise of AI, due in 3 months (it will start from the report done 6 months ago on the topic)
• earlier this summer, the Comité de candidature à l’organisation de l’ICM 2022 issued a communiqué saying that although the IMU had stated a preference for St-Petersburg and that it was customary for other candidacies to withdraw before the next Genral Assembly, they would still present the candidacy of Paris next year…
• a high-quality conference on Differential Geometry will be held at IHÉS next december in memory of the late Marcel Berger
• US-based mathematicians have the opportunity to apply to the collaboration grants of the Simons Foundation announced this week
• Norbert Blum has withdrawn his paper on P vs NP
• today at least Annals of Mathematics is running low on papers in the to appear section (I wonder if an issue ever got delayed due to a lack of accepted papers…)

Logic cookies by Steve Rainwater on flickr

News roundup, and binary Cantor orthogonality

[Posted on august 15, 2017.]

Summer news:

• the extremely sad news that Maryam Mirzakhani died at only 40 ; a memorial took place at Harvard two days ago, and probably others will follow at Stanford and elsewhere
• Sir Michael Atiyah seems to be claiming another big result, but did not post it to the arXiv this time
• John Urschel retired from his pro american football career to concentrate on his PhD at MIT
• Bonn Computer Science Chair Norbert Blum claims a proof of
• MSRI is booked until the summer of 2020 already with lots of attractive programs
• several more prizes for Hugo Duminil-Copin
• Jérôme Germoni has a wide-audience paper (in french) on how easy it is to get a nonsensical paper (generated with mathgen) accepted in a predatory journal
• there is a (french medieval? or earlier?) numeral system that I’d really like to see identified (I currently don’t have access to Ifrah’s encyclopedia, where it may well feature update: I have now checked it and interestingly couldn’t find it, but I found a small comment by S.Lamassé in a more recent book, although not a really convincing one, see my answer in the link. )

***

Completely unrelatedly, here’s probably another useless idea from this blog’s host. Consider a sequence of binary numbers in such that the number of digits of is at least equal to for all . Then one can apply Cantor’s diagonal argument to extract a number that is uniquely defined (since a digit different from must be and vice versa) and different from all the . Call the resulting number the “binary Cantor orthogonal” of that sequence. Can it have any useful properties?

Let’s look at the following example: , the binary version of the inverse of the th prime. That is, we do:

 

then extract the diagonal of the decimal parts and invert it modulo 2. The resulting sequence is 0,0,0,1,1,1,0,0,1,0,1,0,0,1,1,0,0… Unfortunately, the OEIS doesn’t know this particular sequence, so there’s probably nothing noticeable here.

Jardin des Roses in Rennes (a small area of this marvel).

August 2017. Public domain

Euclidean geometry, nominalism, and drawings

[Posted on july 9, 2017.]

In middle and high school, geometry is a very visual affair, always illustrated by drawings. Indeed, reasoning on a problem is usually made much easier by glancing at a sketch, even one not to scale.

Of course, problems can arise if the sketch is not able to capture the essence of the problem, as in the well-known missing square puzzle, which is a good opportunity to tell pupils about the difference between abstract mathematical thinking, and visual “proofs”.

Picture of the puzzle by wikimedia user Krauss

Please note that I am not saying “difference between ideal mathematical objects and their visual approximation” : that would be a Platonistic view, which is not at all compulsory. For instance, a nominalist take on this issue is completely possible, and preferable as far as I’m concerned. See Jody Azzouni’s take in Mathematics, Substance and Surmise: Views on the Meaning and Ontology of Mathematics, in particular the beginning of its section 5:

Now,  in Euclidean geometry we have precise metric statements (a length of , an angle of ), and also some that seem more topological in nature (points belonging to some part of the plane as a consequence of this or that, even though they could also be recast entirely in terms of an angle or length not having some exact value).

So what I’m wondering now is whether there is a framework for approximate geometry, saying that “any set of pseudo-lines [“topological lines”, something not really straight, and of varying thickness, just like on a drawing] and pseudo-points [some “fat dots”], when they are in such and such configuration, imply that another pseudo-line or pseudo-point has a certain property exactly”. In other words, a setting for which every actual drawing on a piece of paper is exactly capturing the essence of the question.

I would be very interested by any relevant comments or references on that topic. Has this been done already?