a new strategy for computing c_n

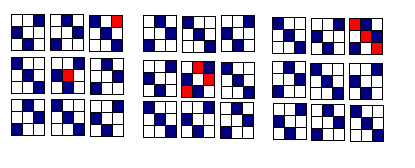
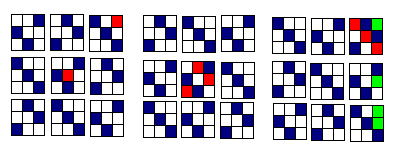
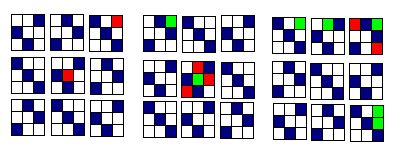
This is a follow-up to this post, were attempts to find a line-free set in with at least 150 elements failed, and where we’ve agreed that programming the search would be better.

Thinking about this I’ve come up with the following strategy (let’s work with but the same can de done with ), I haven’t tested it yet I’m just spelling it out:

1) start with the blank lattice:

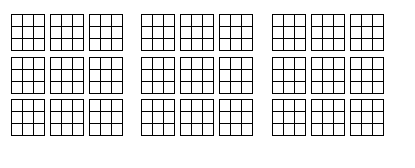
2) then at each lattice site (i.e word ) attach two things: the list of lines it belongs to, and the total number of such lines (a kind of weight, let’s call it )

for example for the lattice site 11111 we have all the following lines:
with one wildcard 1111*, 111*1, 11*11, 1*111, *1111; with two wildcards 111**, 11*1*, 1*11*, *111*, 11**1, 1*1*1, *11*1, 1**11, *1*11, **111; and so on…

3) then order the lattice sites according to their weight from high to low, and remove sites starting from those with highest weight, until the remaining set is line-free.

That is, my idea here is akin to Fourier analysis: do the big features first (here: high intersections, a kind of backbone) then do the fine details (the lines with few intersections, the flesh). Of course for this to work we have to hope that there are “enough” sites with high to moderate weight, so that we can remove as few sites as possible, and that the procedure is “monotone” otherwise all kinds of local minima issues may arise.

I’m going to try out the idea on first to see if we do recover what we already know, and then move on to .

Note in particular that if this idea is correct: the 11..111 site should always be removed since it has the heighest weight, but also that to find the biggest line-free sets for a given one should not re-use the line free sets at but instead recompute the weights and do the search accordingly.

I’ll be offline a few hours and back this afternoon with some code hopefully.

A proof that c_5=154 (?)

After two failed attempts at constructing a line-free 154-element pattern, here is another one which finally seems to work, but requires independent checking:

This represents , where all red and blue squares are not in the set (the red ones being removed in a second run after making sure all blue ones are removing as many lines as possible). The bottom left blue square is 11111, the white one just at its right is 11112, and so on. It seems that all horizontal, vertical, and diagonal lines are indeed prohibited in the end.

Count: . Then, using Michael’s proof that , one concludes that .

I hope somebody will be able to confirm it here. If not, those interested by that method might want to discuss it here without bothering the main 700 thread.

If anything works out then we’d update the wiki, and have a look at to see if some explicit formulation for general can be inferred.

This new pattern above has a lot of permutations into it and as such makes at least more sense that the previous flawed ones.

Edit:
Thanks for the replies, corrections included in green below.

New edit: a few more corrections in green, total count is at 150 now.

Edit: it seems that Terry’s line and another one can both be removed at once by doing some changes.

Unrelatedly another 3 lines were forgotten, so total at 148 now, not even as good as the lower bound by other methods.

Edit: I’m posting a follow-up here: a new programming strategy.