Last october, the CIRM (which has a gorgeous location in the Calanques) has launched its very nice Audiovisual Mathematics Library, featuring HD videos (many being multi-angle, or post-edited — it does lag quite a bit on my connection, but maybe it’s better with a big university broadband network). So I’ve now added that to my previous list.
It also has a youtube channel, with an especially appealing presentation video:
The Hadwiger-Nelson problem is notoriously difficult. (For context see e.g. this text by Michael Payne.) In fact, it seems that the (weaker?) problem to find a 5-chromatic unit distance graph in the plane is still open (see the interesting 2009 Mathematical Coloring Book by Soifer, I couldn’t find more recent improvements online).
Now recall that the Moser Spindle is a 4-chromatic unit distance graph in the plane, and from this set of open problems we have the coordinates of its vertices:
So the idea would be to build on top of that. A first step would be to find a 4-chromatic unit distance graph that has necessarily at least two vertices of the 4th color. And then build further on that one.
So I’ve done some trial and error, and found something that is agonisingly close, namely the following graph on 16 vertices has the correct topology (i.e. a Sage computation gives its minimal set of colored vertices as [[13, 6, 8, 1], [11, 10, 15, 5, 2], [4, 3, 14, 12, 9], [7, 0]], so indeed two vertices of the 4th color), but unfortunately it doesn’t quite have distances 1 everywhere.
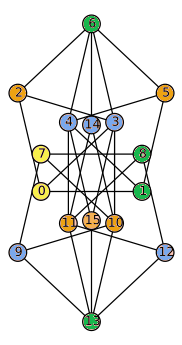
As it happens, if we enforce unit distances at 6~14 and 10~14 then the abscissa of vertex #14 is not 
Edit: Some further tinkering didn’t get anywhere. Removing for simplicity vertices #14 and #15 we do get a 4-chromatic unit distance graph such that at least two vertices have the 4th color.
But I then tried to pack several copies together to increase that number, in the hope that eventually some 5th color must be needed, but it is highly nontrivial: gluing two copies (i.e. some graph that contains 4 spindles) does produce four vertices of the 4th color, but gluing a third that has at least one common vertex with both first copies does not necessarily lead to strictly more than 6 vertices of the 4th color, in my example I still get 6 with the partition [[36, 31, 25, 19, 13, 6, 33, 27, 21, 15, 8, 1], [35, 17, 12, 10, 4, 34, 30, 24, 2], [29, 23, 11, 3, 28, 22, 18, 16, 9, 5], [32, 26, 20, 14, 7, 0]].
Here’s the quick Sage code, in case someone wants to test ideas: first the code of the initial idea with vertices #14 and #15:
from sage.graphs.graph_coloring import chromatic_number
from sage.graphs.graph_coloring import vertex_coloring
from sage.graphs.graph_plot import GraphPlot
from math import sqrt
# hack the Moser spindle
d_3={
0:[1,3,2],
1:[0,4,5],
2:[0,3,6],
3:[0,2,6],
4:[1,5,6],
5:[1,4,6],
6:[2,3,4,5],
7:[8,9,10],
8:[7,11,12],
9:[7,10,13],
10:[7,9,13,3],
11:[8,12,13,4],
12:[8,11,13],
13:[9,10,11,12],
14:[6,10,11],
15:[3,4,13]
}
N=Graph(d_3)
# Now let's compute its chromatic number
N.chromatic_number()
# So N is 4-chromatic like the Moser spindle,
# but let's see if it is better in terms of the number of vertices of color 4 (the Spindle has just one)
# by computing its partition into minimal sets of different colors
vertex_coloring(N, value_only=False, k=None) # or we could similarly do: vertex_coloring(N, value_only=None, k=4)
# So this topology is better in the sense that it must have at least two vertices of color 4
#Let's see now the metric aspect, i.e. whether or not all the length of the edges can be equal 1
vertices_pos_3={}
vertices_pos_3[0]=[0,0]
vertices_pos_3[1]=[1,0]
vertices_pos_3[2]=[(3-sqrt(33))/12,(3*sqrt(11)+sqrt(3))/12]
vertices_pos_3[3]=[(3+sqrt(33))/12,(3*sqrt(11)-sqrt(3))/12]
vertices_pos_3[4]=[(9-sqrt(33))/12,(3*sqrt(11)-sqrt(3))/12]
vertices_pos_3[5]=[(9+sqrt(33))/12,(3*sqrt(11)+sqrt(3))/12]
vertices_pos_3[6]=[0.5,sqrt(11)/2]
vertices_pos_3[7]=[0,(3*sqrt(11)-sqrt(3)-6)/6]
vertices_pos_3[8]=[1,(3*sqrt(11)-sqrt(3)-6)/6]
vertices_pos_3[9]=[(3-sqrt(33))/12,2*((3*sqrt(11)-sqrt(3)-6)/12)-(3*sqrt(11)+sqrt(3))/12]
vertices_pos_3[10]=[(3+sqrt(33))/12,(3*sqrt(11)-sqrt(3)-12)/12]
vertices_pos_3[11]=[(9-sqrt(33))/12,(3*sqrt(11)-sqrt(3)-12)/12]
vertices_pos_3[12]=[(9+sqrt(33))/12,2*((3*sqrt(11)-sqrt(3)-6)/12)-(3*sqrt(11)+sqrt(3))/12]
vertices_pos_3[13]=[0.5,2*((3*sqrt(11)-sqrt(3)-6)/12)-sqrt(11)/2]
vertices_pos_3[14]=[-(895702085/177666094271969928)*sqrt(514527538436665) + (415413875483399597/676176985277553384),
-(19/32519092464)*sqrt(178940893)*sqrt(1427)*sqrt(31)*sqrt(13)*sqrt(5) + (15303925/22788432)]
vertices_pos_3[15]=[-(895702085/177666094271969928)*sqrt(514527538436665) + (415413875483399597/676176985277553384),
2*((3*sqrt(11)-sqrt(3)-6)/12)
+(19/32519092464)*sqrt(178940893)*sqrt(1427)*sqrt(31)*sqrt(13)*sqrt(5) - (15303925/22788432)]
# Explanations:
# 10 is simply a shift of 3 by -1 along y-axis, same with 11 from 4 (i.e. those two edges 10~3 and 11~4 have length 1 by design)
# coordinates of 14 come from the fact that it is located at the intersection of two circles of radius 1 centered at 10 and 6
# so we get them from (we pick the first solution, with lowest y):
#x, y = var('x, y')
#solve([(x-0.5)^2+(y-sqrt(11)/2)^2==1, (x-(3+sqrt(33))/12)^2+(y-(3*sqrt(11)-sqrt(3)-12)/12)^2==1 ], x, y)
# finally the axis of up-down symmetry is y=(3*sqrt(11)-sqrt(3)-6)/12 from which we deduce coordinates of
# 7 from 0, 8 from 1, 9 from 2, 12 from 5, 15 from 14
# So the excruciating problem is that 14 and 15 don't have x=0.5 but only barely so,
# i.e. that topology just barely cannot have all unit distances...
pl = N.graphplot(pos=vertices_pos_3)
pl.show()
And now the topology of the three copies:
from sage.graphs.graph_coloring import chromatic_number
from sage.graphs.graph_coloring import vertex_coloring
from sage.graphs.graph_plot import GraphPlot
from math import sqrt
# hack the Moser spindle
d_3={
0:[1,3,2],
1:[0,4,5],
2:[0,3,6],
3:[0,2,6],
4:[1,5,6,14,16,19],
5:[1,4,6],
6:[2,3,4,5],
7:[8,9,10],
8:[7,11,12],
9:[7,10,13],
10:[7,9,13,3],
11:[8,12,13,4],
12:[8,11,13,20,22,25],
13:[9,10,11,12],
14:[15,16,4],
15:[14,17,18],
16:[14,4,19],
17:[15,18,19],
18:[15,17,19],
19:[4,16,17,18],
20:[21,22,12],
21:[20,23,24],
22:[20,12,25],
23:[21,24,25,17],
24:[21,23,25],
25:[22,12,23,24],
26:[27,4,28],
27:[26,29,30],
28:[26,4,31],
29:[27,30,31],
30:[27,29,31],
31:[28,4,29,30],
32:[33,34,11],
33:[32,35,23],
34:[32,11,36],
35:[33,23,36,29],
36:[34,11,35,23],
}
N=Graph(d_3)
# let's compute its chromatic number
N.chromatic_number()
# let's compute its partition into minimal sets of different colors
vertex_coloring(N, value_only=False, k=None) # or we could similarly do: vertex_coloring(N, value_only=None, k=4)
episodic thoughts 